Paver la sphère

Voici une petite photo que j'ai prise de la Géode, une grande salle de cinéma quasi-sphérique située dans le parc de la Vilette (dans le 19^ème arrondissement de Paris).

Afin de donner un effet "miroir" spectaculaire à leur Géode, les concepteurs (les architectes Adrien Fainsilber et Gérard Chamayou) ont recouvert celle-ci de 6 433 triangles sphériques en acier poli. 

Sauriez-vous y détecter une anomalie ?..

Regardez bien ...

 

Un pentagone sphérique régulier se cache parmi les hexagones sphériques réguliers !

Est-ce une fantaisie des architectes ? Pas sûr...

Dans le plan euclidien:

Dans le plan euclidien, la somme des angles d'un triangle est toujours égale à 180°.

De plus, il n'existe que trois pavages réguliers du plan, constitués uniquement d'un seul type de polygones réguliers, appelés "tuiles"  (triangles équilatéraux, carrés, hexagones réguliers). 

Le plan étant infini, la taille d'une tuile fondamentale du réseau (parmis les trois citées plus haut) importe peu (on peut tout aussi bien paver le plan uniquement avec des triangles équilatéraux de 1 cm de côté comme on le ferait avec des triangles équilatéraux de 15.36 m de côté par exemple). De plus, le nombre de tuile pour réaliser le pavage sera infini.

Si on pave le plan de triangles équilatéraux par exemple, cela donne ceci:

Autour de chaque noeud du réseau obtenu, la somme des angles est de 360° ( = 6 x 60°).

Et en groupant les triangles comme ci-dessous, on obtient un pavage dual constitué d'hexagones réguliers.

Autour de chaque noeud du réseau, la somme des angles est encore de 360° (= 3 x 120 °).

Sur la sphère:

Pour la sphère, il en va autrement !

D'abord, contrairement au plan, la sphère est finie. Si une tuile peut paver la sphère, elle ne peut donc pas être de n'importe-quelle taille (sa surface en particulier doit être inférieure à celle de la sphère, à savoir  4∏R², où R est le rayon de la sphère) .

Autre différence avec le plan, sur la sphère le plus court chemin d'un point A à un autre B (appelé "géodésique") n'est pas la ligne droite, mais est un arc de cercle. Plus précisément un arc de grand cercle passant par A et B dont le centre est le centre O de la sphère, et dont le rayon est OA. 

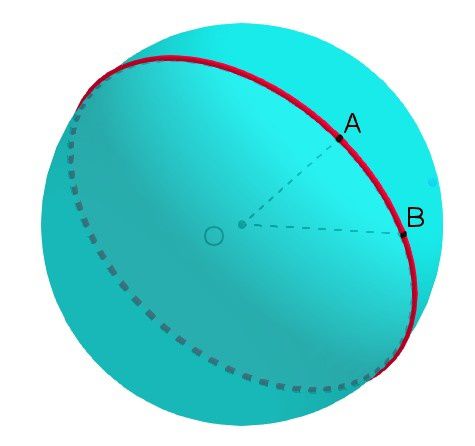
Comme sur le plan, on peut donc créer sur la sphère des triangles, en joignant trois points distincts non alignés de la sphère par des géodésiques. Si AB=BC=AC, le triangle est équilatéral. 

Cependant, la somme des angles d'un triangle "sphérique" est supérieure à 180° (la courbure de la sphère "gonfle" leurs mesures respectives). Et plus l'aire du triangle sphérique sera grande, plus l'écart entre la somme des mesures de ses angles et celle de l'angle plat (180°) sera importante . Les angles d'un "petit" triangle équilatéral sphérique seront donc différents d'un triangle plus grand.

Ce qui, intuitivement, se comprend : en effet, localement, le plan euclidien approxime la sphère ("La Terre est plate!" a-t-on longtemps cru), mais cette approximation est de moins en moins bonne si on augmente l'échelle.

Paver la sphère avec des triangles équilatéraux est possible : il suffit de se servir d'un icosaèdre (polyèdre régulier à 20 faces qui sont des triangles équilatéraux) inscrit dans celle-ci, puis de relier les sommets par des géodésiques. On recouvre alors la sphère par 20 triangles équilatéraux sphériques identiques. Mais leur taille est définie selon le rayon de la sphère. De plus, si on les regroupe par 6, on obtient 3 hexagones, et il reste 2 triangles. 

Plus généralement, on démontre que paver la sphère uniquement par des hexagones réguliers n'est pas possible. Un mix hexagones réguliers/pentagones réguliers sous certaines conditions par contre l'est (comme pour les ballons de foot). 

L'astuce des architecte a donc consisté a utiliser un maximum de triangles équilatéraux identiques (et par suite d'hexagones réguliers), le "reste" formant un pentagone (dont les triangles sont légèrement différents, car cinq triangles équilatéraux ne forment pas un pentagones).

Avoir placé ce pentagone bien en vue a-t-il été fait volontairement ?.. Il faudrait le demander aux auteurs...

 N.B. : les sphères ci-dessus ont été réalisées avec Geogebra 5.0, qui comporte maintenant un module 3D, longtemps      attendu !